-
LU Descomposition
Although is certianly represents a sound way to solve such systems, it become inefficient when solving equations with the same coefficients [A], but with different rignt-hand-side constants (the b's). Recall that Gauss elimination involves two steps: foward elimination and backsubstitution. Of these, the foward elimination step comprimeses the bulk of the computational effort. This is a particulary true for large systems of equations. LU descompositions methods separate the time - consuming elimination of the matrix [A] from the manipulations of the right side hand vectors can be evaluated in an efficient manner. Interestingly, Gauss elimination ifself can be expressed as LU descomposition. Before showing how this can be done, let us a first provide a mathematical overview of the descomposition strategy.
Overview of LU Descomposition
Just as was the case with Gauss elimination, LU descomposition requires pivoting to avoid division by zero. However, to simplify the following description, we will defer the issue of pivoting until after the fundamental approach is elaborated. In addition, the following explanation is limited to a set of three simultaneous equations. The results can be directly extended to n-dimensional systems.
Although is certianly represents a sound way to solve such systems, it become inefficient when solving equations with the same coefficients [A], but with different rignt-hand-side constants (the b's). Recall that Gauss elimination involves two steps: foward elimination and backsubstitution. Of these, the foward elimination step comprimeses the bulk of the computational effort. This is a particulary true for large systems of equations. LU descompositions methods separate the time - consuming elimination of the matrix [A] from the manipulations of the right side hand vectors can be evaluated in an efficient manner. Interestingly, Gauss elimination ifself can be expressed as LU descomposition. Before showing how this can be done, let us a first provide a mathematical overview of the descomposition strategy.
Overview of LU Descomposition
Just as was the case with Gauss elimination, LU descomposition requires pivoting to avoid division by zero. However, to simplify the following description, we will defer the issue of pivoting until after the fundamental approach is elaborated. In addition, the following explanation is limited to a set of three simultaneous equations. The results can be directly extended to n-dimensional systems.
[A] {x} - {B} = 0 (1)
Suppose that equation (1) could be expressed as an upper and triangular system
Recognize that this is similar to the manipulation that occurs in the first step of Gauss elimination. That is, elimination is used to reduce the system to upper to triangular form.Equation (2) can also be expressed in matrix notation and rearrange to give,
[U][X]-[D]=0 (3)
Now, assume that there is a lower diagonal matrix with 1's on the diagonal,
that is the property that when the equation (3) is premultiplied by it, equation (1) is the result.
That is,
[L]{{U}{X} - {D}}=[A]{X} - {B} (5)
If this equation hold, it follows from the rules of matrix multiplication that[L][U]=[A] (6) and [L][D]=[B] (7)
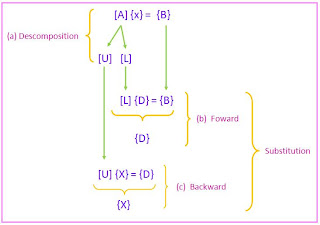
A two step strategy for obtaining solutions can be based on equations (3) (6),and (7)
- LU descomposition step. [A] is factored of "descomposed" into Lower [L] and Upper [U] triangular matrices.
- Substitution step- [L] and [U] are used to determine a solution {X} for a right hand side {B}. This step ifself consists of two steps. First, equation (7) is used to generate an intermediate vector {D} by forward substitution. Then, the result is substituted into the equation (3), wich can be solved with back sustitution for {X}.
LU Decomposition Version of Gauss Elimination
Although it might appear at face value to be unrelated to LU decomposition, Gauss elimination can be used to decompose [A] into [L] and [U]. This can be easily seen for [U], which is direct product of the forward elimination. Recall that the forward-elimination step is intended to reduce the original coefficient matrix [A] to the form
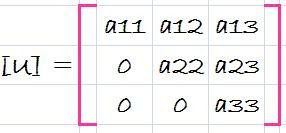 wich is in desired upper triangular format.
wich is in desired upper triangular format.Though is might not be as apparent, the matrix [L] is also produced during the step. This can be readily illustrated for a three-equations system,
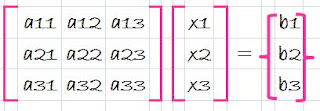
The first step in Gauss elimination is to multiply row 1 by the factor [recall Eq. 12]
f21= a21/a11
and substract the result from the secoond row to eliminate a21. Similarly, row 1 is multiplied by
f31=a31/a11
and the result subtracted from the third row to eliminate a31. The final step is to multiply the modified second row byf32= a32/a22
and subtract the result from the third row to eliminate a32.
Now suppose that we merely perform all these manipulations on the matrix [A]. Clearly, if we do not want to change the equation, we also have to do the same to the right-hand side {B}. But there is absolutely no reason that we have to perform the manipulations simultaneously. Thus, we could save the f's and manipulate {B} later.
Where do we store the factors f21, f31 and f32? Recall that the whole idea behind the elimination was to created zeros in a21, a31, and a32. Thus, we can store f21 in a21, f31 in a31, and f32 in a32. After elimination, the [A] matrix can therefore be written as
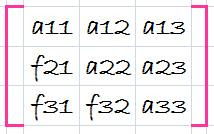
This matrix, in fact, represents an efficient storage of the LU decomposition of [A],
[A] -> [L][U]
where
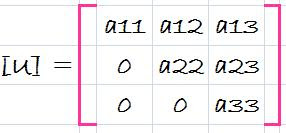 and
and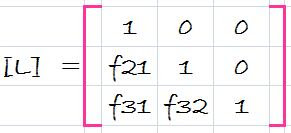 source: chapra 5th edition
source: chapra 5th edition


3 comments:
THE METHOD IS VERY SIMPLE, THANK YOU FOR INFORMATION, I DIDN'T UNDERSTAND IT BEFORE READ YOUR BLOG
BUT, WHAT CASE CAN YOU USE THE LU DESCOMPOSITION AND MATRIX INVERSION?
I'm glad, we are here for everyone' learning, include my learning too
Post a Comment