Excell's Templates

.

Hi, if you want a see or use some of my templates, here they are!

Just, download for a view in Excell's format

TEMPLATE 1

Contents: Bisection method, linear interpolation, Newton Raphson's method, Secant method and substitution

http://s3.amazonaws.com/ppt-download/plantillametodos-100727004936-phpapp01.xls?Signature=oc8Tdu4JMsAQ%2BsAjrwApR2TgUuM%3D&Expires=1280210248&AWSAccessKeyId=AKIAJLJT267DEGKZDHEQ

Autor: Carlos Andrés Uribe Hidalgo

TEMPLATE 2

Contents: Fixed point

http://s3.amazonaws.com/ppt-download/puntofijo-100727013552-phpapp01.xlsx?Signature=l9EcYr6VgQ%2FYv9KTNVjztBEuRx0%3D&Expires=1280213242&AWSAccessKeyId=AKIAJLJT267DEGKZDHEQ

Autor: Marcela Andrea Carrillo

 

TEMPLATE 3

Contents: Fixed point, Secant method, bisection method, false position method and Newton Raphson's method

http://s3.amazonaws.com/ppt-download/metododebiseccion-100727011748-phpapp01.xlsx?Signature=MU4sNyejwIqz7woSpanHIn9mR54%3D&Expires=1280211912&AWSAccessKeyId=AKIAJLJT267DEGKZDHEQ

Autor: Luis Carlos Molina, Brian Leonardo Gil

TEMPLATE 4

Contents: Secant method and Newton Raphson's Method

http://s3.amazonaws.com/ppt-download/metodosabiertos-100727012527-phpapp02.xlsx?Signature=Ym1sfjcKHUhMa6NtXWGqFmKcuk4%3D&Expires=1280212480&AWSAccessKeyId=AKIAJLJT267DEGKZDHEQ

Autor: Arcadio Cuy

Cholesky decomposition

:

LU Descomposition and matrix inversion

-

LU Descomposition

Although is certianly represents a sound way to solve such systems, it become inefficient when solving equations with the same coefficients [A], but with different rignt-hand-side constants (the b's). Recall that Gauss elimination involves two steps: foward elimination and backsubstitution. Of these, the foward elimination step comprimeses the bulk of the computational effort. This is a particulary true for large systems of equations. LU descompositions methods separate the time - consuming elimination of the matrix [A] from the manipulations of the right side hand vectors can be evaluated in an efficient manner. Interestingly, Gauss elimination ifself can be expressed as LU descomposition. Before showing how this can be done, let us a first provide a mathematical overview of the descomposition strategy.

Overview of LU Descomposition

Just as was the case with Gauss elimination, LU descomposition requires pivoting to avoid division by zero. However, to simplify the following description, we will defer the issue of pivoting until after the fundamental approach is elaborated. In addition, the following explanation is limited to a set of three simultaneous equations. The results can be directly extended to n-dimensional systems.

[A] {x} - {B} = 0 (1)

Suppose that equation (1) could be expressed as an upper and triangular system

(2)

Recognize that this is similar to the manipulation that occurs in the first step of Gauss elimination. That is, elimination is used to reduce the system to upper to triangular form.Equation (2) can also be expressed in matrix notation and rearrange to give,

[U][X]-[D]=0 (3)

Now, assume that there is a lower diagonal matrix with 1's on the diagonal,

(4)

that is the property that when the equation (3) is premultiplied by it, equation (1) is the result.

That is,

[L]{{U}{X} - {D}}=[A]{X} - {B} (5)

If this equation hold, it follows from the rules of matrix multiplication that

[L][U]=[A] (6) and [L][D]=[B] (7)

A two step strategy for obtaining solutions can be based on equations (3) (6),and (7)

1. LU descomposition step. [A] is factored of "descomposed" into Lower [L] and Upper [U] triangular matrices.
2. Substitution step- [L] and [U] are used to determine a solution {X} for a right hand side {B}. This step ifself consists of two steps. First, equation (7) is used to generate an intermediate vector {D} by forward substitution. Then, the result is substituted into the equation (3), wich can be solved with back sustitution for {X}.

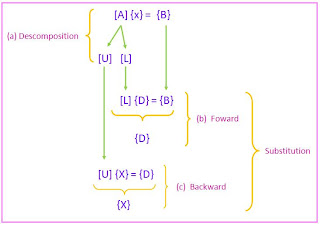
LU Decomposition Version of Gauss Elimination

Although it might appear at face value to be unrelated to LU decomposition, Gauss elimination can be used to decompose [A] into [L] and [U]. This can be easily seen for [U], which is direct product of the forward elimination. Recall that the forward-elimination step is intended to reduce the original coefficient matrix [A] to the form

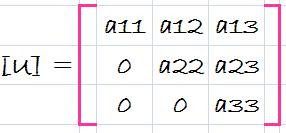wich is in desired upper triangular format.

Though is might not be as apparent, the matrix [L] is also produced during the step. This can be readily illustrated for a three-equations system,

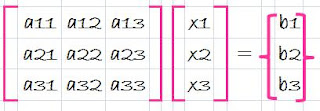
The first step in Gauss elimination is to multiply row 1 by the factor [recall Eq. 12]

f21= a21/a11

and substract the result from the secoond row to eliminate a21. Similarly, row 1 is multiplied by

f31=a31/a11

and the result subtracted from the third row to eliminate a31. The final step is to multiply the modified second row by

f32= a32/a22

and subtract the result from the third row to eliminate a32.

Now suppose that we merely perform all these manipulations on the matrix [A]. Clearly, if we do not want to change the equation, we also have to do the same to the right-hand side {B}. But there is absolutely no reason that we have to perform the manipulations simultaneously. Thus, we could save the f's and manipulate {B} later.

Where do we store the factors f21, f31 and f32? Recall that the whole idea behind the elimination was to created zeros in a21, a31, and a32. Thus, we can store f21 in a21, f31 in a31, and f32 in a32. After elimination, the [A] matrix can therefore be written as


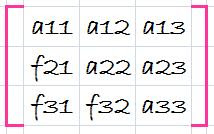
This matrix, in fact, represents an efficient storage of the LU decomposition of [A],

[A] -> [L][U]
where
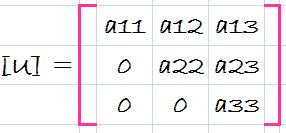and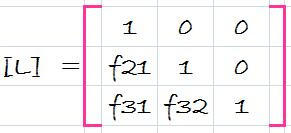

source: chapra 5th edition

Direct Methods For The Solution Of Systems Of Equations

-

The Engineer of Universidad Industrial de Santander, UIS, Bucaramanga, Colombia, Elkin Santafe, based in his knowledge and his research, give to us a little summary about direct methods for the solution of systems of equations

Direct Methods For The Solution Of Systems Of Equations

View more presentations from Marcela Carrillo.